Sommario anno XIII numero 7 - luglio 2004

Le ipotesi non euclidee - 10a puntata   (di Luca Nicotra)
2. Saccheri, “vindex” di Euclide.
Giovanni Gerolamo Saccheri, fervido seguace di Euclide, nell’anno stesso in cui morì, il 1733, diede alle stampe la sua opera Euclides ab omni naevo vindicatus, concepita con l’intenzione di dimostrare il quinto postulato e in tal modo “liberare” (in latino vindicare) da ogni difetto gli Elementi del grande matematico alessandrino. Nello stesso tempo, derivando quel postulato dai precedenti, per tutti evidenti e quindi “veri”, credette di consacrare finalmente la verità eterna e assoluta della geometria euclidea, dissipando qualsiasi dubbio sulla sua validità che potesse nascere da quel famigerato postulato. Infatti, se non si fosse riusciti a dimostrarlo, o ancor peggio se si fosse riusciti a dimostrarne la indimostrabilità, ci si sarebbe dovuti rassegnare, come genialmente in realtà aveva fatto Euclide stesso¹, ad accettarlo come postulato, ma sarebbe rimasta impregiudicata la sua mancanza di evidenza e quindi il suo difetto di verità, essendo nel pensiero filosofico-scientifico di quei tempi vero soltanto ciò che ha una realtà oggettiva, fisica, e pertanto risulta evidente e manifesto a tutti. Per tali motivi, ci si sarebbe trovati di fronte ad una situazione paradossale: da una parte la costrizione ad accettarlo come postulato, dall’altra la riluttanza a farlo, in ossequio al concetto di vero fino ad allora  imperante. Inoltre, il dubbio della verità del quinto postulato avrebbe inficiato altre parti degli Elementi di Euclide, che di esso si servono per la dimostrazione di vari teoremi, con lo sconsolante effetto di veder crollare la millenaria fede nell’unica geometria fino ad allora conosciuta, che non sarebbe stata più “affidabile”.
Saccheri cercò di conseguire il suo scopo applicando il tipo di ragionamento proprio delle dimostrazioni per assurdo, di cui già si è detto in queste pagine, e ch’egli illustrò magistralmente in una sua precedente operetta intitolata Logica, ponendone in rilievo tutta la generalità e le feconde applicazioni².
Indichiamo con:
·           a l’insieme delle proposizioni primitive euclidee;
·           con S(a) l’insieme delle proposizioni derivabili da a, vale a dire la geometria costruita sopra a (geometria euclidea);
·           con E il quinto postulato, che fa parte di a;
·           con a’ l’insieme delle proposizioni primitive euclidee nel quale E è sostituito dalla sua negazione non-E, vale a dire a’= a - E + “non-E”;
·           con S(a’) l’insieme delle proposizioni derivabili da a’, vale a dire la geometria costruita sopra a’ (geometria non-euclidea³).

Nel caso in questione, Saccheri seguì questo tipo di ragionamento: se E fosse un teorema, e quindi fosse derivabile dalle rimanenti proposizioni primitive a – E, farebbe parte oltre che di S(a), anche di S(a’). Infatti, poiché S(a’) contiene tutte le proposizioni derivate da a’= a - E + “non-E”,  conterrebbe anche E, come teorema derivabile dalle proposizioni a – E. Dunque, la geometria S(a’) sarebbe contraddittoria, poiché conterrebbe due proposizioni che sono la negazione l’una dell’altra: E, non-E. In altre parole la geometria S(a’) costituita dalle prime 28 proposizioni di Euclide + la negazione del quinto postulato + tutte le proposizioni derivate risulterebbe contraddittoria perché conterrebbe la negazione del quinto postulato e il quinto postulato stesso, che, come teorema, sarebbe conseguenza delle prime 28 proposizioni degli Elementi. Dunque, per dimostrare che il quinto postulato E è un teorema, è sufficiente mostrare che la geometria non-euclidea S(a’) è contradditoria. In base a queste osservazioni Saccheri, non soltanto avrebbe emendato gli Elementi da ogni “difetto”, ma avrebbe parimenti celebrato il trionfo della geometria euclidea, che sarebbe risultata inequivocabilmente l’unica geometria coerente e possibile, risultando false le altre due geometrie concepibili⁴, fondate  sulle due possibili negazioni del quinto postulato e sui rimanenti della geometria euclidea. Ma Saccheri commise l’errore di iniziare le sue considerazioni da una forma equivalente del quinto postulato che si proponeva di  dimostrare: la cosiddetta ipotesi dell’angolo retto.
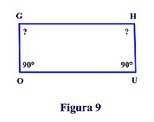Con riferimento alla figura 9, per le estremità di un segmento OU si conducano due segmenti OG, UH uguali e perpendicolari ad OU, e infine si tracci la congiungente GH. Al lettore, ora, si chiede uno sforzo d’immaginazione: la figura ottenuta non deve essere considerata come un rettangolo (cosa che verrebbe spontanea a tutti di fare!), poiché dal punto di vista logico ciò implicherebbe l’ammissione che gli angoli OGH e UHG siano retti. La nostra mente non deve essere condizionata dai “suggerimenti” che provengono dall’osservazione della figura disegnata sul piano euclideo a noi divenuto familiare e che ci porterebbe senza esitazione ad affermare essere retti i due angoli suddetti. In realtà, l’unica cosa che sappiamo è che i due angoli GOU e HUO sono retti per costruzione, ma nulla sappiamo sugli angoli OGH e UHG, per i quali, quindi, possiamo legittimamente prendere in considerazione le tre possibilità seguenti: retti, acuti, ottusi. Ebbene, è possibile dimostrare, senza far uso del postulato delle parallele, ma soltanto dei precedenti quattro postulati, che quegli angoli sono uguali ma non che sono retti o acuti od ottusi. Invece, servendosi del postulato delle parallele, si dimostra che gli angoli OGH e UHG sono retti e, viceversa, se si ammette come postulato che sono retti allora si deduce la proposizione nota come postulato delle parallele. Dunque il postulato delle parallele (vale a dire il quinto postulato euclideo) e il postulato dell’angolo retto (cioè il postulato che gli angoli OGH e UHG siano retti) sono equivalenti, perché interdeducibili.
Le tre ipotesi dell’angolo retto, acuto ed ottuso si escludono a vicenda ed esauriscono tutti i casi possibili relativi alla natura dei due angoli OGH e UHG. Pertanto, le ultime due ipotesi, dell’angolo acuto e dell’angolo ottuso, costituiscono i due soli modi di negare il quinto postulato. Saccheri, sostituendo separatamente quest’ultimo con quelle ipotesi, costruì due nuove geometrie, dette “geometria dell’angolo acuto” e “geometria dell’angolo ottuso”, mirando a mostrare la loro contraddittorietà e quindi la falsità di ciascuna di esse. Egli, però, da quel grande logico che era, fin quando seguì la via del più rigoroso ragionamento, non riuscì a trovare alcuna contraddizione. A un certo punto, però, il tono delle sue argomentazioni inspiegabilmente muta e da irreprensibili diventano oscure e inconcludenti a proposito della geometria dell’angolo acuto, che Saccheri condanna come falsa. La geometria dell’angolo ottuso, a sua volta, viene da lui liquidata come falsa, grazie ad un uso improprio degli infinitesimali.
Il grande matematico italiano Eugenio Beltrami, riscopritore dell’Euclides ab omni naevo vindicatus, rimase perplesso davanti ad una così clamorosa inversione di marcia, proprio quando le circostanze avrebbero dovuto far emettere a Saccheri un giudizio di coerenza su ciascuna delle due nuove geometrie. L’impressione  che se ne ricava è una deliberata capitolazione dinanzi alla sconcertante verità di quei due nuovi mondi geometrici tanto diversi da quello euclideo, ritenuto fino ad allora l’unico possibile. “O Saccheri era ben risoluto a sacrificare la propria ragione sull’altare della fede in Euclide, oppure non osava confessare la sua fede in una geometria eretica. Questo repentino ripudio di ogni elementare principio di logica colpì il laico Beltrami come un’offesa all’ordine naturale delle cose. Un logico dell’acutezza di Saccheri, egli si disse, non poteva assolutamente essere giunto a quella conclusione, non avrebbe mai potuto, fin tanto che la sua mente fosse in grado di funzionare. Perché dunque fingeva di averla accettata?La risposta è immediata: paura. Saccheri non osava insinuare che la nuova geometria era vera. Euclide, il geometra senza menda, era sacro quasi quanto Aristotile, il logico infallibile. Negare Euclide sarebbe stato lo stesso che mettere in dubbio la logica classica, grazie alla quale erano stati fissati per tutta l’eternità i dogmi fondamentali della teologia ufficiale. Sostenere che un sistema non euclideo potesse essere vero al pari di quello d’Euclide, sarebbe stato un invito temerario alle repressioni e ai provvedimenti disciplinari. Per questo il Copernico⁵ della geometria ricorse al sotterfugio: denunciò egli stesso la falsità della sua scoperta, sperando che questo pio tradimento gli valesse l’indulgenza della censura e quindi il permesso di stampare il libro.”⁶
La dimostrazione⁷ di verità geometriche diverse avrebbe fatto perdere alla geometria d’Euclide il suo monopolio millenario ed ogni carattere di assolutismo. Si trattava dunque di una presa di posizione che avrebbe avuto gravi ripercussioni, attaccando ancora una volta, e ancor più che nel caso della rivoluzione copernicana, il gretto conservatorismo intellettuale che viveva di assoluti.
“L’Euclide poteva si essere falso, e falso l’aveva definito Saccheri, forse nella disperata speranza che la sua storica scoperta non perisse con lui, ma restava pur sempre un libro troppo carico di significati e di suggestioni perché si potesse lasciarlo circolare liberamente. Così chiaro e convincente era il ragionamento del Saccheri nell’esposizione delle nuove geometrie, che ogni mente razionale, nel seguire quelle dimostrazioni seducenti, poteva soggiacere a pensieri illeciti. Pur lasciando impregiudicata la questione se il libro sia stato deliberatamente soppresso, è certo che una politica conservativa, per essere coerente con se stessa, avrebbe dovuto procedere alla sua soppressione per ragioni di sicurezza. I suoi insegnamenti erano antitetici a quelli di coloro che ne avevano autorizzato la stampa ed è noto che quando un organismo si divide in due parti contrastanti, le sue probabilità di sopravvivenza sono minime.⁸"           

(Fine della 10a puntata)

Note:
1 Proprio per tale riconoscimento, la critica moderna assegna ad Euclide un posto d’onore nella storia della matematica, e non tanto per il presunto valore logico della sua opera, in realtà, come accennato precedentemente, lacunoso.
2 Già Gerolamo Cardano e il Clavio avevano illustrato, ma con minor efficacia, tale tipo di ragionamento nelle loro opere.
3 A rigore per geometria non-euclidea si dovrebbe intendere una qualunque geometria fondata su postulati differenti da quelli euclidei. Nell’uso corrente, invece, tale denominazione si riserva alle due geometrie fondate sulla sostituzione del quinto postulato con le sue due possibili negazioni e sui rimanenti postulati euclidei.
4 All’epoca, l’unico dubbio sulla geometria euclidea riguardava la verità del quinto postulato, mentre nulla si aveva da obiettare sui rimanenti postulati; per questi, quindi, non c’era alcuna ragione di sostituirli con altri. 
5 Il titolo di “Copernico della geometria” fu dato dall’inglese W. K. Clifford al matematico russo N. Lobachewsky quando non era ancora nota l’opera di Saccheri. Per molte analogie, oltre che per diritto di priorità, il titolo spetta più a Saccheri che a  Lobachewsky. Infatti, per sfuggire alla persecuzione ecclesiastica, Copernico , ecclesiastico come Saccheri, presentò la sua teoria come semplice congettura e vide la prima copia della sua opera quand’era già sul letto di morte. Analoghe circostanze si ripeterono per Saccheri, che fece “stampare” e non “pubblicare” la sua opera l’anno stesso che morì. La semplice stampa non seguita da una vera pubblicazione fu il motivo dell’oblio in cui cadde l’Euclides ab omni naevo vindicatus.
6 Eric Temple Bell, La magia dei numeri, capitolo XXV.
7 La dimostrazione della validità logica delle geometrie non-euclidee fu data, molto più tardi, da Eugenio Beltrami e da Felix Klein.
8 Eric Temple Bell, La magia dei numeri , cap. XXV

Sommario anno XIII numero 7 - luglio 2004